Nuestro sistema originó en India, y llegó al mundo
occidental por los imperios árabes. Usamos el base 10; hay diez símbolos para representar 10 dígitos diferentes. Casi
claramente, la selección del diez estaba relacionada con el número de los dedos humanos.
Los diez signos son los dígitos comunes, como 0, 3 y 9. En el sistema, la posición de los dígitos determina el valor; este concepto era distinto de muchos números tempranos como los de los romanos.
Esencialmente, cada posición tiene su propio valor, que aumenta exponencialmente
desde la derecha hasta la izquierda. Por ejemplo, la posición de la extrema
derecha tiene un valor de uno y la próxima posición a la derecha tiene un valor de diez. Puedes
ver esta situación a la derecha.
En la imagen, podemos ver el valor
del dígito 3 en tres posiciones distintas, y este mismo dígito tiene un
valor diferente en cada posición. Por ejemplo, el primero desde la derecha vale tres, pero el último vale 300; estos valores son resultados de sus posiciones. Esta diferencia es el base de los sistemas
posicionales.
Otra vista del valor del número aparece
en esta ecuación:
En la ecuación, empezamos con el
dígito de la extrema derecha y lo multiplicamos por el base 10 elevado al
exponente de su posición, que es inicialmente cero. Este resultado es el valor
de este dígito, y sumamos este número con nuestra suma hasta ahora, que es cero
al principio. Después, nuestra suma es tres, y entonces repetimos este proceso
con el proximo dígito a la izquierda hasta que no haya más dígitos. La posición del
dígito aumenta en incrementos de uno durante cada paso. De esta manera,
obtenemos un valor de 333 de este número, como anticiparíamos.
En este sistema, el uso del cero como un parámetro de sustitución es importante. Porque el valor del dígito
depende de la posición, el marcador de las posiciones no importantes juega un papel crucial. Sin usar el cero para marcar los dígitos sin una contribución a la
suma, sería imposible distinguir entre algunos números. Por ejemplo, con el
cero, los números 801 and 81 claramente son diferentes, pero, sin el cero, no
hay una diferencia entre los dos. En ese caso, 801 pueden ser escrito como 8 1 o
8 1 o aún 81, y por eso, no es fácil interpretar los números sin el cero. Generalmente, el uso del cero de este modo provee una
manera fácil y normalizada para representar todos los números, así que es un
concepto importante en el campo matemático.
Puedes leer un poco más sobre el sistema decimal en este enlace:
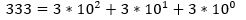
No comments:
Post a Comment