El sistema maya contaba
con el valor posicional, pero sus valores estaban basados en el base 20 en vez
de 10. Probablemente, la selección del veinte estaba relacionado con el número
combinado de los dígitos humanos.
Este sistema vigesimal funcionaba como el sistema decimal en la mayor parte, pero había algunas diferencias entre los dos.
Primero, el sistema maya no tenía veinte signos diferentes; en vez de
eso, los mayas solamente usaban tres símbolos: un por el cero, un por el uno
y un por el cinco. El signo por el cero era usualmente un tipo de concha,
aunque a veces usaban otros símbolos como una cabeza por el cero. El signo por el uno era un punto, que
representaba una piedra. Finalmente, el signo por el cinco era una raya larga,
que representaba un palo. Este valor probablemente estaba relacionado con el
número de los dedos de una mano. Los tres signos están arriba. De esta manera,
todos los signos mayas estaban basados en algunos objetos de su medio ambiente.
Combinaron estos símbolos para crear todos los números entre el cero y el
diecinueve. Los dígitos mayas están abajo, excepto el cero.
Formaban los dígitos con los tres signos por sumar los
valores de los símbolos. Por ejemplo, se representaba el número 13 con dos
rayas y tres puntos de este modo:
Simplificaban los dígitos por reemplazar cinco puntos con una raya. De este modo, cada dígito entre el cero y el diecinueve podía ser representado únicamente. Estas veinte
representaciones funcionaban como nuestros dígitos.
Próximo, los mayas usaban el valor
posicional de una manera diferente de nosotros. Se expresaban los números de abajo
arriba, así que la posición con el valor más pequeño se ubicaba en el pie del
número. Aparte de eso y del base 20, el sistema maya seguía la misma idea como el sistema decimal. Un ejemplo aparece abajo a la izquierda.
Este número tiene tres dígitos; de abajo arriba, éstos
son 0, 17 y 2. Empezamos en el dígito más abajo y lo multiplicamos por el valor de esta posición, que es uno en la primera posición.
Entonces, sumamos este resultado con nuestra suma hasta ahora, que es
inicialmente el cero. En este caso, no sumamos nada con este dígito porque es cero, así que nuestra suma permanece cero. Entonces, avanzamos al próximo
dígito más arriba; en nuestro caso, es diecisiete. Multiplicamos otra
vez, con el valor posicional, pero esta vez el valor posicional es el veinte, así que llegamos al
valor de 340. Entonces, la suma es 340, y de alguna manera similar,
obtenemos un resultado de 1140 en nuestro sistema decimal. Es importante
recordar que, para los mayas, los valores posicionales son los exponentes del
veinte; este fenómeno ocurre por el base 20. De esta forma, podemos calcular
algún número representado con los dígitos mayas de las conchas, los puntos y
las rayas.
Otra vista matemática de esto usa
los exponentes directamente:
El exponente del veinte aumenta de
abajo arriba, que resulta en los valores posicionales como uno, veinte, 400 y 8000. Estos valores corresponden a uno, diez, 100 y 1000 en nuestro sistema. Por eso, desde el punto de vista del
panorama general, el sistema de los mayas y el de los hindús son muy similares;
solamente difieren en el base, los símbolos específicos y el orden de los
dígitos.
Puedes leer más de la historia maya
y de sus números en este enlace:
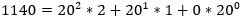
No comments:
Post a Comment